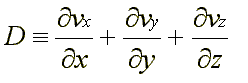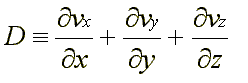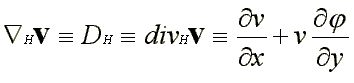Konvergence a divergence proudění
©Tomáš Psika. Napsáno dne 6.9.2001
Divergence proudění je v meteorologii stěžejním pojmem, který se používá v mnoha rovnicích při modelování zemské atmosféry a podílí se na vývoji tlakových útvarů a má velký význam pro prostorový rozptyl látek znečišťujících ovzduší. Cílem této krátké eseje je poskytnout základní přehled o této fyzikální vlastnosti proudění, tak aby byl snáze pochopitelný i pro laiky a meteorology-amatéry.
Zájemce o meteorologii, který se podívá do meteorologického slovníku (Meteorologický slovník výkladový & terminologický, vydalo Ministerstvo životního prostředí ČR, Praha 1993) na pojem divergence proudění, bude asi velmi zklamán. Zde se tento stěžejní pojem vysvětluje jen pouhým srovnáváním konvergence a divergence prostřednictvím hodnot vypočítaných pomocí tohoto vzorce:
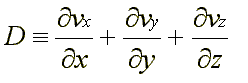
Tento výraz však neřekne vůbec nic tomu, kdo nemá lepší znalosti matematiky a ani člověk se sebevětší představivostí si nebude s tímto nesmyslem moc lámat hlavu. Vzorec vyjadřuje sice úplně přesně to, co divergence je, ale naprosto nepřehledně. Pokusme se nejdříve vysvětlit laicky a pomocí obrázků, co to divergence je.
Zprvu je třeba pochopit, že pojem divergence se používá ve dvou významech. My si nejdřív vysvětlíme širší význam tohoto slova. Vzorec uvedený výše vyjadřuje divergenci proudění v tzv. standardní souřadné soustavě (tj. kartézské soustavě souřadnic se středem v bodě ležícím v rovině tečné k zemskému povrchu, viz obr. 1, kdy kladný směr osy x směřuje k východu, osa y směřuje k severu a osa z směrem vzhůru) a my se jím dále nebudeme zabývat.
Divergence v širším významu slova může být záporná (D<0), pak mluvíme o konvergenci, nebo kladná (D>0), a pak mluvíme o divergenci v užším smyslu. Následující tři obrázky ukazují vektory rychlosti při konvergenci proudění (zanedbáváme zatím svislou osu z a rychlosti větru jsou konstantní):



Jak je patrné, tak ke konvergenci proudění dochází zejména tehdy, když dochází ke sbíhání (konfluenci) vektorů větru. Analogicky pak dochází k divergenci při rozbíhání proudnic, jak ukazují další tři obrázky:


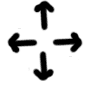
Můžeme tedy říci, že při sbíhání větru při zemi dochází ke konvergenci a při rozbíhání větru zase k divergenci. To bychom však potom mohli zaměnit pojmy konvergence s konfluencí a divergencí s difluencí. To ale neplatí pokud uvažujeme to, že se rychlost větru časem mění. Pak zjistíme, že ke konvergenci dochází tehdy, když se rychlost větru snižuje, k divergenci pak v opačném případě. Konvergenci, resp. divergenci pak zobrazují tyto dva obrázky:


Lze tedy říci, že ke konvergenci proudění dochází tehdy, když se snižuje rychlost větru nebo dochází ke sbíhání větru a v opačných případech dochází k divergenci. Nemůže se ale stát, že by např. docházelo k rozbíhání větru při zemi a přitom ke zpomalování větru? Samozřejmě, že může a v atmosféře se tomu tak také často děje. Jak pak rozhodnout, zda jde o konvergenci nebo o divergenci? V tomto případě je nutné provést výpočet pomocí některého vzorce (např. podle prvního zmíněného).
Divergence (v širším významu slova) se tedy skládá z dvou komponent:
1. změna rychlosti větru,
2. sbíhavost větru.
Kdybychom pojmy konvergence a divergence měly přeložit do srozumitelné češtiny, nejspíš správným termínem by bylo vtékání, resp. vytékání vzduchu. A právě tato vlastnost má vliv na promíchávání vzduchu. Při konvergenci totiž dochází k vtékání vzduchu do určitého místa a ten pak nemůže nikam jinam než nahoru, vytváří tedy výstupné proudy. Divergence naopak působí sestupné proudy, které zamezují tvorbě konvekčních oblaků (např. kumulů) a znesnadňují vertikální promíchávání vzduchu. Právě zde pak můžeme najít souvislost s rozložením pole divergence v tlakových útvarech. Ke konvergenci dochází proto často v oblastech
nízkého tlaku vzduchu, kde převládají výstupné proudy, a k divergenci pak často v oblastech tlakových výší.
Vše, co jsme si zatím o divergenci řekli, se týká tzv. horizontální divergence, která se týká pouze zemského povrchu. Meteorologové však častěji pracují s prostorovou divergencí. Na dalších obrázcích je znázorněné, jak vypadá divergence v atmosféře.
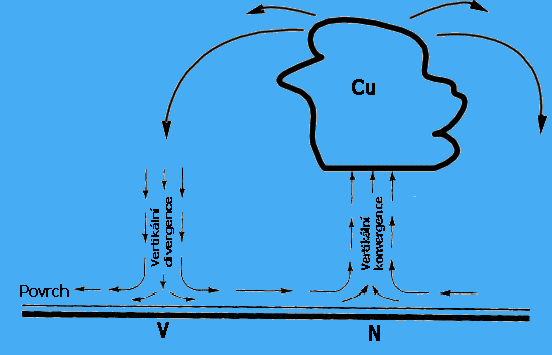
Nejvíc se konvergentní pohyby v atmosféře projevují při výskytu bouřek, kdy se oblast konvergence situuje do části výstupného proudu, silnou konvergenci lze najít i v hurikánech. Asi nejvýznamnější oblast divergentního proudění spojeného s velmi silným nárazovitým větrem můžeme každoročně vidět při bouřkových lijácích před silnými studenými frontami. Tato oblast divergentního proudění se vyskytuje nejčastěji v oblasti srážek (nemusí být nutně vázána na srážky) pod "zralým" bouřkovým oblakem. Tuto situaci znázorňuje další obrázek. Při této situaci dochází pod bouřkovým oblakem k prudkým sestupným proudům v důsledku např. vypadávání krup, kdy se síla větru směrem k zemi zvyšuje a navíc díky výskytu tzv. "bouřkové anticyklóny" dochází k prudké rozbíhavosti proudění při zemi, tj. vede to vše k silné divergenci.

Pokud jde o matematickou stránku věci, tak horizontální divergence v přirozených souřadnicích (rovina stejná jako u standardní soustavy souřadnic, jen osa x směřuje ve směru proudění a osa y je kolmo nalevo od směru vektoru větru) vypadá takto:
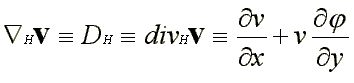
První člen v této rovnici na pravé straně vyjadřuje zrychlení větru, čili dokazuje, že se zvyšováním rychlosti větru se divergence zvyšuje, druhý člen pak vyjadřuje změnu úhlu sevřeného vektorem větru a vektorem směřujícím k východu (osa x standardního souř.systému) při změně proudění ve směru osy y přirozené soustavy. Tento druhý člen pak produkuje divergenci při zvětšení této odchylky, tj. při rozbíhání proudnic.
Pozn.: divergence je operace, při které se skalárně násobí vektor s gradientem pozorované veličiny, v případě divergence proudění jde o součin gradientu a vektoru rychlosti.
Použité zdroje: